使用 RMarkdown 的 child 参数，进行文档拼接。
这样拼接以后的笔记方便复习。
相关问题提交到 Issue

WOE和IV的作用：

度量线性关系，WOE度量是否有，IV度量强度
进行分类变量和连续变量的比较，这里类似于信息增益（也可以进行分类变量和连续变量的比较）
因为WOE的计算需要将连续变量离散化，因此input一定都是分类变量，因此缺失值也是一个类别，可以计算WOE和IV

1 信息熵

1.1 信息量

信息量的定义 (机器学习算法与自然语言处理 2018)

一个事件的信息量就是这个事件发生的概率的负对数。

加入一个事件有n个可能性，每个可能性相当，因此出现任意一个可能性的概率为\(\frac{1}{n}\)。那么负对数。当一件事情的发生概率越小，信息量越大，\(\frac{1}{n} \downarrow\)，\(-\log\)是减函数，因此信息量 \(-\log(\frac{1}{n})\)上升。

而且满足可加性。假设两个概率\(x\) 和 \(y\)一同发生的概率为\(xy\)（变得更小了），因此信息量更大。 \[-\log(x) - \log(y) = - \log(xy)\] \[-\log(x) - \log(y|x) = - \log(x(y|x))\]

1.2 直观理解

Shannon (1948) 给予了概率分布的信息熵的定义。信息熵描述的混乱(disorder)的程度，更直观的理解是不确定性(uncertainty)的程度 (Larsen 2015)。因此，

高信息熵等价于高不确定性性，高异质性¹
低信息熵等价于低不确定性性，低异质性²

1.3 公式理解

信息量 \(h(x) = \log(\frac{1}{p(x)})\)如此定义，主要反映几个特征 (Oshima 2016)。

\(h(x) \geq 0\)，信息的得到是一个正数的概念。
\(p(x) \uparrow \to \frac{1}{p(x)} \downarrow \to h(x) \downarrow\)，衡量一件事情发生概率越大，因此给人的信息量越小。

因此关于概率的加权期望就是信息熵³，衡量一个变量的信息量的期望。

\[H(X) = \sum p(x)\log\frac{1}{p(x)}\]

最后一个自变量的划分，导致Y变量前后信息熵的变化越大，体现自变量的信息增益越高。

2 Mutual information

Shannon and Weaver (1949) 给予了 Mutual information的定义。⁴

\[MI(X,Y) = H(X) + H(Y) - H(X,Y)\]

直观理解是这种不确定性的下降作为Mutual information。

3 WOE Weight of Evidence

这就是我们普遍计算 WOE 和理解的公式

\[\underbrace{\log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}} = \log \frac{\frac{P(Y=1|X_j)}{P(Y=1)}}{\frac{P(Y=0|X_j)}{P(Y=0)}}\]

因此

\[\log\frac{P(Y=1|X_j)}{P(Y=0|X_j)} = \overbrace{\log\frac{P(Y=1)}{P(Y=0)}}^{\text{sample odds}} + \underbrace{\log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}}\]

\[\underbrace{\log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}} = f(X_j | Y={0,1}) = f(X_j | Y)\]

因此这就是一个回归模型的特征变量。

因此很容易理解\(WOE=0\)的情况，

\[0 = \log \frac{\frac{P(Y=1|X_j)}{P(Y=1)}}{\frac{P(Y=0|X_j)}{P(Y=0)}}\] \[1 = \frac{\frac{P(Y=1|X_j)}{P(Y=1)}}{\frac{P(Y=0|X_j)}{P(Y=0)}}\]

\[\frac{P(Y=1|X_j)}{P(Y=0|X_j)} = \overbrace{\frac{P(Y=1)}{P(Y=0)}}^{\text{sample odds}}\]

也就是\(X_j\)作为一个分类，毫无用处。\(Y\)和\(X_j\)独立。

4 WOE的优点和缺点

4.1 优点

通过对连续变量的切分和分类变量的合并，使得新的类别和\(y\)保持单调性
分类变量的合并，减少了自由度的损失
利于变量之间的比较，(更好的是使用IV，因为WOE没有考虑组内的样本大小，详见 SmartEDA 包测评)

4.2 缺点

通过对连续变量的切分和分类变量的合并，损失了信息
没有考虑\(x\)之间的相关性
连续变量的切分，可能导致过拟合

参考 King Solomon’s Horse, Stack Exchange

5 和朴素贝叶斯和逻辑回归的关系

5.1 逻辑回归

我们可以发现以上公式是一个逻辑回归的格式。

截距

\[\overbrace{\log\frac{P(Y=1)}{P(Y=0)}}^{\text{sample odds}}\]

\(\beta\)为0

\[\underbrace{\log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}}\]

5.2 朴素贝叶斯

因此这里进行拓展到多个变量，便是朴素贝叶斯公式 (Statistical Learning 2009)，

\[\log\frac{P(Y=1|X_1,\cdots,X_p)}{P(Y=0|X_1,\cdots,X_p)} = \overbrace{\log\frac{P(Y=1)}{P(Y=0)}}^{\text{sample odds}} + \underbrace{\sum_{i=1}^p \log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}}\]

朴素贝叶斯假设\(x\)之间独立，因此这里每个\(x\)跟\(Y\)之间的相关性都为1，没有强弱之分。

\(\underbrace{\sum_{i=1}^p \log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}}\) 就相当于一组特征变量。

5.3 半参数朴素贝叶斯

\[\log\frac{P(Y=1|X_1,\cdots,X_p)}{P(Y=0|X_1,\cdots,X_p)} = \overbrace{\log\frac{P(Y=1)}{P(Y=0)}}^{\text{sample odds}} + \underbrace{\sum_{i=1}^p \beta_j \log \frac{f(X_j|Y=1)}{f(X_j|Y=0)}}_{\text{WOE}}\]

这里使用每个WOE作为\(x\)，进行逻辑回归的训练，得到每个\(x\)跟\(Y\)的\(\beta\)关系，这里假设了\(x\)之间不独立⁵。

这里的\(\beta\)是 5.2 公式的推广，但是\(\beta\)不满足恒大于0。

5.3.1 \(\forall \beta > 0\)?

如果\(\beta\)存在负的，是否应该剔除？先说答案，不应该。这是一个典型的计量错误。

换句话说，这是调参的问题，

Is there a difference between ‘controlling for’ and ‘ignoring’ other variables in multiple regression? (Stack Exchange 2013)

在多元回归中，控制其他变量不变和忽略其他变量，两者有什么区别？

这里的区别就是

控制其他变量不变，就是做多元回归，在这里\(\beta\)会产生负数
忽略其他变量，就是做简单的相关性检验，在这里\(\beta\)恒大于0。

由5.3公式，我们可以简化为更一般的模型，

\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \mu\]

假设这里\(x_1\)和\(x_2\)代表了一众WOEs，且和\(y\)是正相关的，是否能够说明，因为这里的\(\hat \beta_2\)为负的，就删除\(x_2\)。显然是不能够的。

\(x_1\)和\(x_2\)代表了一众WOEs，且和\(y\)是正相关的，这是忽略其他变量的分析
\(\hat \beta_2\)为负的，这是控制其他变量不变的分析

两者不是同一分析，因此结果也没有可比性。

产生\(\beta <0\)的情况，这里给予公式推导和图形推理，两种方式理解。

5.3.2 公式推导

由3公式可知，sample odds是一个常数，因此WOE和\(\log\frac{P(Y=1|X_j)}{P(Y=0|X_j)}\)是完全线性正相关，因此，

\[\forall \beta > 0\]

但是实际操作中，会发生

\[\exists \beta < 0\]

这里举例说明，

\[\log\frac{P(Y=1|X)}{P(Y=0|X)} = \beta_0 + \beta_1 WOE_1 + \beta_2 WOE_2 + \mu\]

简化为

\[z = \beta_0 + \beta_1 WOE_1 + \beta_2 WOE_2 + \mu\]

回归得到，

\[\hat z = \hat \beta_0 + \hat \beta_1 WOE_1 + \hat \beta_2 WOE_2\]

化简得到，

\[\hat \beta_2 = \frac{\hat z -\hat \beta_0 - \hat \beta_1 WOE_1 + }{WOE_2}\]

已知，

\(\hat z\)和\(WOE_2\)完全正相关
\(\hat \beta_0\)为0，
\(\hat \beta_1\)符合假设大于0

那么这里只能是

\(WOE_1\)和\(WOE_2\)线性正相关导致的。

但是OLS假设中，并未要求所有的\(x\)完全非线性相关，因此这里不足以给出剔除\(WOE_2\)的依据。

5.3.3 图形分析

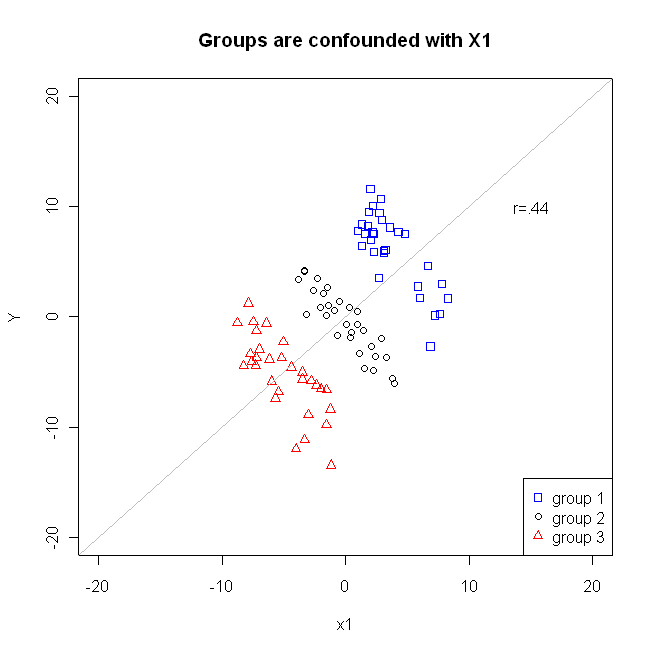
如图，x1和Y相关系数为0.44，为正。(Stack Exchange 2012) 当加入变量group后，我们发现在每个group里面，x1和Y的相关性为负的。

当控制变量group后，x1关于Y的回归系数为负的。

5.4 信息值

\[IV_j = (P(X_j|Y=1)-P(X_j|Y=0) \times WOE_j\]

6 Uplift modeling

Uplift modeling 用于比较测试组和对照组的区别。⁶

Net weight of evidence (NWOE) (Larsen 2015) 为

\[\begin{alignat}{2} NWOE &= WOE_t - WOE_c \\ &= \underbrace{\log \frac{f(X_j|Y=1)_t}{f(X_j|Y=0)_t}}_{\text{treatment WOE}} - \underbrace{\log \frac{f(X_j|Y=1)_c}{f(X_j|Y=0)_c}}_{\text{control WOE}} \\ &= \frac{ \overbrace{f(X_j|Y=1)_t}^{\text{treatment}} \overbrace{f(X_j|Y=0)_c}^{\text{control}} }{ \underbrace{f(X_j|Y=1)_c}_{\text{control}} \underbrace{f(X_j|Y=0)_t}_{\text{treatment}} } \end{alignat}\]

t - treatment
c - control

\[NIV = ( \overbrace{f(X_j|Y=1)_t}^{\text{treatment}} \overbrace{f(X_j|Y=0)_c}^{\text{control}} - \underbrace{f(X_j|Y=1)_c}_{\text{control}} \underbrace{f(X_j|Y=0)_t}_{\text{treatment}} ) \times NWOE\]

7 External Cross Validation

7.1 penalty

当做Cross Validation时，我们可以定义penalty(Larsen 2015)为⁷

\[\begin{alignat}{2} WOE_{\text{train}} - WOE_{\text{valid}} &= NWOE \\ &=\text{penalty} \end{alignat}\]

因此，假设有k folds，

\[\text{total CV penalty} = (P(X_j|Y=1)-P(X_j|Y=0)) \sum_{i=1}^k \text{penalty}_i\]

\[\begin{alignat}{2} \text{adj.IV}_j &= IV_j - \text{total CV penalty} \\ &= \overbrace{(P(X_j|Y=1)-P(X_j|Y=0)) \times WOE_j}^{IV_j} - \underbrace{(P(X_j|Y=1)-P(X_j|Y=0)) \sum_{i=1}^k \text{penalty}_i} _{\text{total CV penalty}} \\ &= (P(X_j|Y=1)-P(X_j|Y=0)) [WOE_j - \sum_{i=1}^k \text{penalty}_i] \end{alignat}\]

8 WOE 的兼顾性

1.问：什么我们做评分卡的时候要用woe编码，而不是用别的编码方式呢？比如onehot之类的，仅仅是因为woe可以把特征从非线性变成线性的吗？ (梅子行 2020) 答：因为onehot后高维稀疏，模型学习是有困难的。一般模型会做embedding，但是做了embedding就不可解释了。这不符合某些风控场景的解释性要求。所以用woe来代替。当然WOE有一点点的过拟合倾向，但是对分类变量来说，依旧是业内最佳实践方案。 (梅子行 2020)

onehot 太稀疏，embedding 解释性不强，因此 WOE 是折中比较好的方法，兼顾非稀疏和解释性。

9 和树模型重要性的比较

20.问：xgb变量重要性用哪一个指标？ (梅子行 2020) 4、xgb筛选特征可以理解为用均方差最小来做特征筛选，和IV、WOE属于同一种筛选方式，，描述的都是特征对分类任务的贡献度，一般用一个就行了，每个人的方法都不一样，见仁见智。 (梅子行 2020)

均方差最小来做特征筛选，那么 XGB 和 IV、WOE 都很类似，因此描述的结果类似，但是正负结果没法把握。

10 计算

library(SmartEDA)
library(tidyverse)
library(ISLR)
library(formattable)
library(knitr)
library(DT)
Carseats <- ISLR::Carseats

10.1 计算WOE值的函数

table(Carseats$Urban)

## 
##  No Yes 
## 118 282

names(Carseats)

##  [1] "Sales"       "CompPrice"   "Income"      "Advertising" "Population" 
##  [6] "Price"       "ShelveLoc"   "Age"         "Education"   "Urban"      
## [11] "US"

cat_stats <-
    ExpCatStat(
        Carseats,
        Target = "Urban",
        result = "IV",
        clim = 10,
        nlim = 5,
        Pclass = "Yes"
    )
dim(cat_stats)

## [1] 80 12

因此只展示一个变量

cat_stats %>% head(3) %>% 
    kable()

Variable	Class	Out_1	Out_0	TOTAL	Per_1	Per_0	Odds	WOE	IV	Ref_1	Ref_0
ShelveLoc.1	Bad	74	22	96	0.26	0.19	0.85	0.31	0.02	Yes	No
ShelveLoc.2	Good	57	28	85	0.20	0.24	0.81	-0.19	0.01	Yes	No
ShelveLoc.3	Medium	151	68	219	0.54	0.58	1.55	-0.07	0.00	Yes	No

Variable – variable name - 变量名称
Target – Target variable label - 因变量
class – name of bin (variable value otherwise) - 自变量类别
out0 – number of good observations - 正样本数量
out1 – number of bad observations - 负样本数量
Total – Total values for each category - 类别中样本数量
pct1 – good observations / total good observations - 正样本比例
pct0 – bad observations / total bad observations - 负样本比例
odds – pct1/pct0 - 发生比
woe – Weight of Evidence – calculated as ln(odds) - WOE
iv – Information Value - ln(odds) * (pct0 – pct1) - IV

10.1.1 WOE和IV的理解

这里举例计算WOE和IV。

WOE(定义可参考CSDN博客) 类似于信息熵，也是考虑了异质性，当异质性越高，WOE越大，异质性参考章节 1。 \[IV = WOE \times (p_T - p_N) = (\ln(p_T)-\ln(p_N)) \cdot (p_T - p_N)\] 这是一个变量分了很多level，因此我们再\(\sum\)就好了。这里用IV不用WOE，是考虑了样本大小的问题。因为WOE是两个比例的比值，还是比例，也就是不考虑样本大小的。但是比例就不同了，比例是这个特定样本和总体样本的比值，这就是考虑了样本大小的了，所以更好，即使WOE好，但是适合的样本很小，那么IV也很小。

WOE = 异质性，WOE + 规模 = IV

以ShelveLoc变量为例，一共有三个类别

Bad
Good
Medium

以类别Bad为例，改subset下，有

\(y = 1\)的样本为 74 个
\(y = 0\)的样本为 22 个

因此一共有96个样本

样本的正负比例为

Carseats %>% 
    group_by(Urban,ShelveLoc) %>% 
    summarise(n = n()) %>% 
    spread(Urban, n) %>% 
    kable()

ShelveLoc	No	Yes
Bad	22	74
Good	28	57
Medium	68	151

因此

\[\text{Per_1} = \frac{74}{282} = 0.2624113\] \[\text{Per_0} = \frac{22}{118} = 0.1864407\]

因此

\[WOE = \log(\text{Per_1}) - \log(\text{Per_0}) = 0.3418002\]

如果变量内正负分布比整体差异越大，说明这个变量区分度越强。

因此

\[IV_i = (\text{Per_1} - \text{Per_0})[\log(\text{Per_1}) - \log(\text{Per_0})] = 0.0259668\]

然后把三个类别的IV都求解出来

最后

\[IV_{\text{ShelveLoc}} = 0.026 + 0.006 + 0.003 = 0.035\]

这个值可以在 10.2中得到验证。

10.2 计算IV值的函数

ExpCatStat(
    Carseats,
    Target = "Urban",
    result = "Stat",
    clim = 10,
    nlim = 5,
    Pclass = "Yes",
    plot = TRUE
) %>% 
    kable()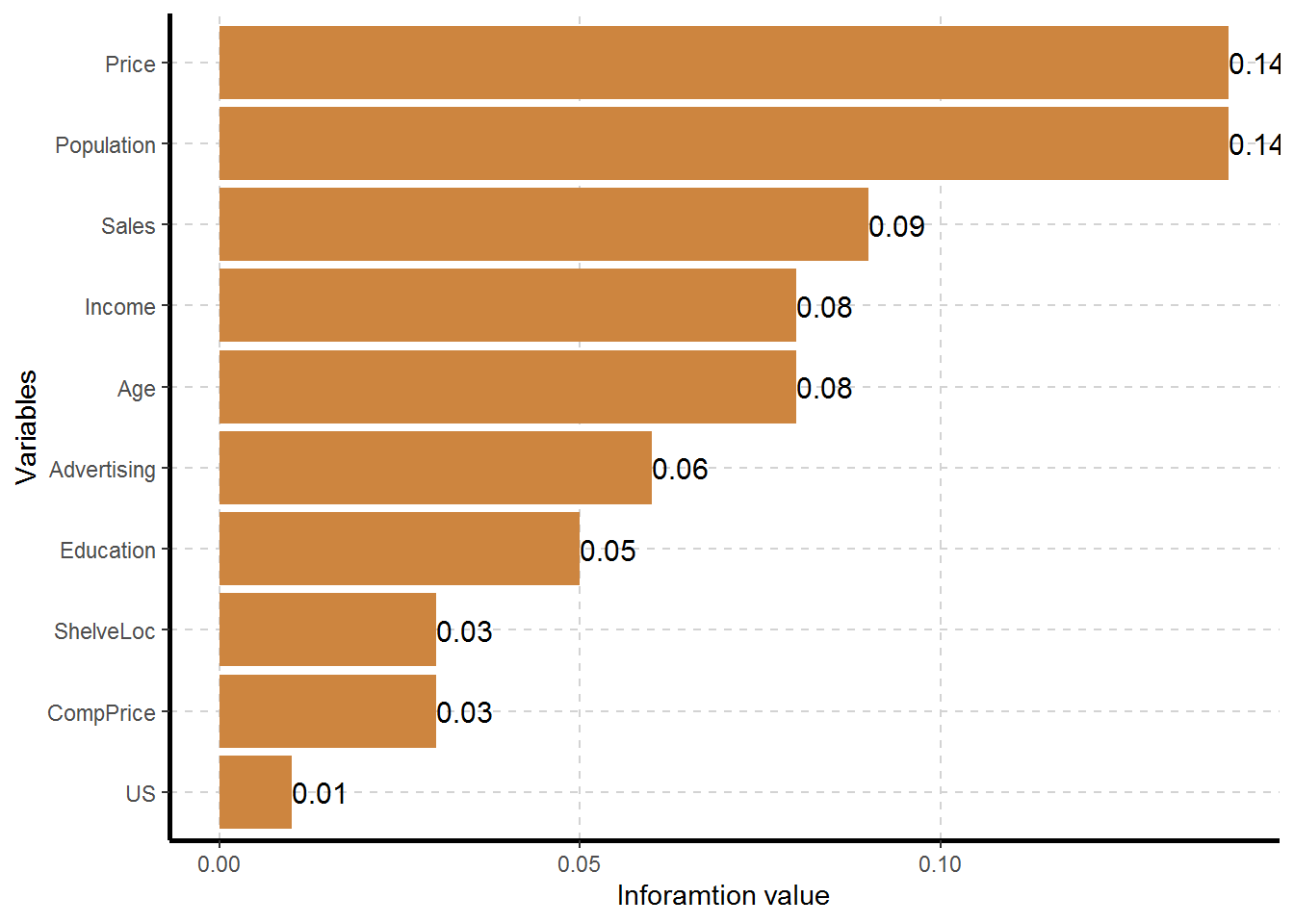

Variable	Target	Unique	Chi-squared	p-value	df	IV Value	Cramers V	Degree of Association	Predictive Power
ShelveLoc	Urban	3	2.738	0.254	2	0.03	0.08	Very Weak	Not Predictive
US	Urban	2	0.684	0.408	1	0.01	0.04	Very Weak	Not Predictive
Sales	Urban	10	6.696	0.669	9	0.09	0.13	Weak	Somewhat Predictive
CompPrice	Urban	10	4.543	0.872	9	0.03	0.11	Weak	Not Predictive
Income	Urban	10	8.428	0.492	9	0.08	0.15	Weak	Not Predictive
Advertising	Urban	7	5.565	0.474	6	0.06	0.12	Weak	Not Predictive
Population	Urban	10	10.560	0.307	9	0.14	0.16	Weak	Somewhat Predictive
Price	Urban	10	11.143	0.266	9	0.14	0.17	Weak	Somewhat Predictive
Age	Urban	10	8.414	0.493	9	0.08	0.15	Weak	Not Predictive
Education	Urban	8	5.122	0.645	7	0.05	0.11	Weak	Not Predictive

If information value is < 0.03 then predictive power = “Not Predictive”
If information value is 0.3 to 0.1 then predictive power = “Somewhat Predictive”
If information value is 0.1 to 0.3 then predictive power = “Meidum Predictive”
If information value is >0.3 then predictive power = “Highly Predictive”
If information value is >0.5 then predictive power = “Suspicious Predictive Power”

附录

参考文献

Larsen, Kim. 2015. “Data Exploration with Weight of Evidence and Information Value in R.” 2015. https://multithreaded.stitchfix.com/blog/2015/08/13/weight-of-evidence/.

Oshima, Noriko. 2016. “如何通俗的解释交叉熵与相对熵?” 2016. https://www.zhihu.com/question/41252833.

Shannon, Claude Elwood. 1948. “A Mathematical Theory of Communication.” Bell System Technical Journal.

Shannon, Claude Elwood, and Warren Weaver. 1949. “The Mathematical Theory of Communication.” University of Illinois Press.

Stack Exchange. 2012. “Positive Correlation and Negative Regressor Coefficient Sign.” 2012. https://stats.stackexchange.com/questions/34151/positive-correlation-and-negative-regressor-coefficient-sign.

———. 2013. “Is There a Difference Between ’Controlling for’ and ’Ignoring’ Other Variables in Multiple Regression?” 2013. https://stats.stackexchange.com/questions/78828/is-there-a-difference-between-controlling-for-and-ignoring-other-variables-i#78830.

Statistical Learning, Elements of. 2009. Hastie, Trevor , Tibshirani, Robert and Friedman, Jerome. Springer.

机器学习算法与自然语言处理. 2018. “我就不信看完这篇你还搞不懂信息熵.” 2018. https://mp.weixin.qq.com/s/7NrB0UtmELXD3UNO3C6jGA.

梅子行. 2020. “偷偷潜入了风控大佬的技术交流群，曝光最硬核的聊天记录.” 大数据风控与机器学习. 2020. https://mp.weixin.qq.com/s/F7jbT2hNvOolBd4yIh-GVA.

正如投掷硬币，正反各为50%的概率，因此信息熵很高，不确定性很高，因此信息就很少，没用 (Larsen 2015)。↩
因此，高信息熵差值越大，表达了不确定性降低程度越高。如果split后的两节点的同质性分别提高，说明该特征变量好。
- \(\Box\)合并那篇文章。
↩
entropy 英 [ˈɛntrəpi]↩
\(\Box\) Mutual information 和WOE的联系↩
\(\Box\)更加一般的模型是generalized additive model (GAM)模型，这里不展开讨论。↩
\(\Box\)这个可以结合算\(\Delta y\)，跟 do nothing 作为比较。↩
\(\Box\)如果penalty很高，可能的原因是，样本内差异很大，方差很高？ \(\Box\)可以使用包进行NWOE的计算，NIV的计算，推荐检验一波先。Information包↩

WOE 和 IV 学习笔记