图神经网络 学习笔记

李家翔

2020-03-15

1. 使用 RMarkdown 的 child 参数，进行文档拼接。
2. 这样拼接以后的笔记方便复习。
3. 相关问题提交到 Issue

dmlc/dgl的 Python 包，实现起来还不错。

1 Minimal Example

参考 Wang et al. (2019) 和 苘郁蓁 (2019)

# !pip install dgl

%matplotlib inline
%run build_karate_club_graph.py

G = build_karate_club_graph()
print('We have %d nodes.' % G.number_of_nodes())
print('We have %d edges.' % G.number_of_edges())

We have 34 nodes.
We have 156 edges.

import networkx as nx
nx_G = G.to_networkx().to_undirected()
pos = nx.kamada_kawai_layout(nx_G)
nx.draw(nx_G, pos, with_labels=True, node_color=[[.7, .7, .7]])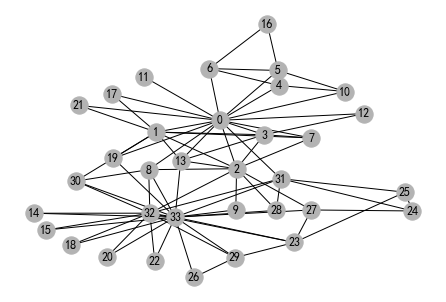

png

# 将每个节点的特征转化成one-hot向量
import torch

G.ndata['feat'] = torch.eye(34)

print(G.nodes[2].data['feat'])

tensor([[0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])

print(G.nodes[[10, 11]].data['feat'])

tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])

%run GCNLayer.py

<Figure size 432x288 with 0 Axes>

# 以空手道俱乐部为例
# 第一层将34层的输入转化为隐层为5
# 第二层将隐层转化为最终的分类数2
net = GCN(34, 5, 2)

inputs = torch.eye(34)
labeled_nodes = torch.tensor([0, 33])  # only the instructor and the president nodes are labeled
labels = torch.tensor([0, 1])  # their labels are different

optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
all_logits = []
for epoch in range(30):
    logits = net(G, inputs)
    # we save the logits for visualization later
    all_logits.append(logits.detach())
    logp = F.log_softmax(logits, 1)
    # we only compute loss for labeled nodes
    loss = F.nll_loss(logp[labeled_nodes], labels)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))

Epoch 0 | Loss: 0.9486
Epoch 1 | Loss: 0.7210
Epoch 2 | Loss: 0.5390
Epoch 3 | Loss: 0.3941
Epoch 4 | Loss: 0.2917
Epoch 5 | Loss: 0.2103
Epoch 6 | Loss: 0.1471
Epoch 7 | Loss: 0.0991
Epoch 8 | Loss: 0.0656
Epoch 9 | Loss: 0.0420
Epoch 10 | Loss: 0.0268
Epoch 11 | Loss: 0.0171
Epoch 12 | Loss: 0.0111
Epoch 13 | Loss: 0.0073
Epoch 14 | Loss: 0.0049
Epoch 15 | Loss: 0.0034
Epoch 16 | Loss: 0.0023
Epoch 17 | Loss: 0.0016
Epoch 18 | Loss: 0.0012
Epoch 19 | Loss: 0.0009
Epoch 20 | Loss: 0.0006
Epoch 21 | Loss: 0.0005
Epoch 22 | Loss: 0.0004
Epoch 23 | Loss: 0.0003
Epoch 24 | Loss: 0.0003
Epoch 25 | Loss: 0.0002
Epoch 26 | Loss: 0.0002
Epoch 27 | Loss: 0.0001
Epoch 28 | Loss: 0.0001
Epoch 29 | Loss: 0.0001

# %load draw.py
import matplotlib.animation as animation
import matplotlib.pyplot as plt

def draw(i):
    cls1color = '#00FFFF'
    cls2color = '#FF00FF'
    pos = {}
    colors = []
    for v in range(34):
        pos[v] = all_logits[i][v].numpy()
        cls = pos[v].argmax()
        colors.append(cls1color if cls else cls2color)
    ax.cla()
    ax.axis('off')
    ax.set_title('Epoch: %d' % i)
    nx.draw_networkx(nx_G.to_undirected(), pos, node_color=colors,
            with_labels=True, node_size=300, ax=ax)

fig = plt.figure(dpi=150)
fig.clf()
ax = fig.subplots()
draw(0)  # draw the prediction of the first epoch
# plt.close()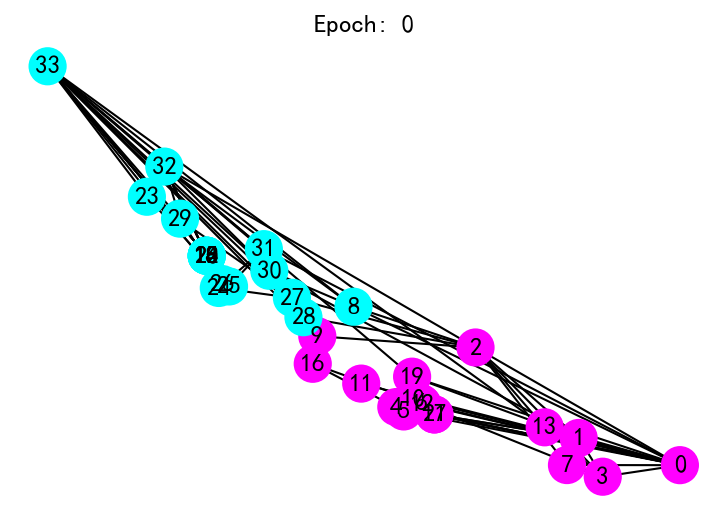

png

ani = animation.FuncAnimation(fig, draw, frames=len(all_logits), interval=200)
ani.save('../output/GCN.gif')
plt.show()

MovieWriter ffmpeg unavailable; trying to use <class 'matplotlib.animation.PillowWriter'> instead.

2 node2vec

import pandas as pd
import numpy as np
import itertools
from sklearn.cluster import KMeans
import pprint

2.1 Prepare input for node2vec

We’ll use a CSV file where each row represents a single recommendable item: it contains a comma separated list of the named entities that appear in the item’s title.

一个样本为一个序列特征。

named_entities_df = pd.read_csv('named_entities.csv')
named_entities_df.head()

	named_entities
0	basketball,Kobe Bryant
1	basketball,Lebron James

First, we’ll have to tokenize the named entities, since node2vec expects integers.

处理成节点特征。

tokenizer = dict()
named_entities_df['named_entities'] = named_entities_df['named_entities'].apply(
    lambda named_entities: [tokenizer.setdefault(named_entitie, len(tokenizer))
                            for named_entitie in named_entities.split(',')])
named_entities_df.head()

	named_entities
0	[0, 1]
1	[0, 2]

pprint.pprint(list(tokenizer.items())[0:5])

[(‘basketball’, 0), (‘Kobe Bryant’, 1), (‘Lebron James’, 2)]

In order to construct the graph on which we’ll run node2vec, we first need to understand which named entities appear together.

pairs_df = named_entities_df['named_entities'].apply(lambda named_entities: list(itertools.combinations(named_entities, 2)))
pairs_df = pairs_df[pairs_df.apply(len) > 0]
pairs_df = pd.DataFrame(np.concatenate(pairs_df.values), columns=['named_entity_1', 'named_entity_2'])
pairs_df.head()

	named_entity_1	named_entity_2
0	0	1
1	0	2

Now we can construct the graph. The weight of an edge connecting two named entities will be the number of times these named entities appear together in our dataset.

pairs_df.groupby(['named_entity_1', 'named_entity_2']).size().reset_index(name='weight')

	named_entity_1	named_entity_2	weight
0	0	1	1
1	0	2	1

NAMED_ENTITIES_CO_OCCURENCE_THRESHOLD = 0
# By default, 25

edges_df = pairs_df.groupby(['named_entity_1', 'named_entity_2']).size().reset_index(name='weight')
edges_df = edges_df[edges_df['weight'] > NAMED_ENTITIES_CO_OCCURENCE_THRESHOLD]
edges_df[['named_entity_1', 'named_entity_2', 'weight']].to_csv('edges.csv', header=False, index=False, sep=' ')
# 为了作为文本输入，这里需要按照`' '`进行切分
# https://github.com/aditya-grover/node2vec/issues/42
edges_df.head()

	named_entity_1	named_entity_2	weight
0	0	1	1
1	0	2	1

Next, we’ll run node2vec, which will output the result embeddings in a file called emb.
We’ll use the open source implementation developed by Stanford.

!python node2vec/src/main.py --input edges.csv --output emb --weighted

Walk iteration: 1 / 10 2 / 10 3 / 10 4 / 10 5 / 10 6 / 10 7 / 10 8 / 10 9 / 10 10 / 10

2.2 Read embedding and run KMeans clusterring:

emb_df = pd.read_csv('emb', sep=' ', skiprows=[0], header=None)
emb_df.set_index(0, inplace=True)
emb_df.index.name = 'named_entity'
emb_df.head()

	1	2	3	4	5	6	7	8	9	10	…	119	120	121	122	123	124	125	126	127	128
named_entity
0	-0.017839	-0.015540	0.014009	0.011204	0.001812	0.016809	-0.029363	0.019553	0.017015	-0.042528	…	0.005440	0.007404	0.008619	-0.002957	0.007757	-0.027168	0.001521	0.009814	0.003208	-0.026657
1	-0.015903	-0.012227	0.009864	0.006678	0.006132	0.015084	-0.021753	0.011210	0.015354	-0.031373	…	0.009581	0.000854	0.009060	-0.001659	0.005635	-0.015787	-0.001362	0.005597	0.005464	-0.018249
2	-0.014181	-0.006827	0.011194	0.001440	0.001613	0.013619	-0.019055	0.011773	0.012155	-0.028162	…	0.006589	0.003170	0.002821	-0.004832	0.001820	-0.018488	0.004074	0.000793	0.003839	-0.017300

3 rows × 128 columns

emb_df.shape

(3, 128)

Each column is a dimension in the embedding space. Each row contains the dimensions of the embedding of one named entity.

每一列是一个 embedding 的维度。

We’ll now cluster the embeddings using a simple clustering algorithm such as k-means.

下面利用 embedding 进行聚类。

NUM_CLUSTERS = 2
# By default 10

kmeans = KMeans(n_clusters=NUM_CLUSTERS)
kmeans.fit(emb_df)
labels = kmeans.predict(emb_df)
emb_df['cluster'] = labels
clusters_df = emb_df.reset_index()[['named_entity','cluster']]
clusters_df.head()

	named_entity	cluster
0	0	1
1	1	0
2	2	0

2.3 Prepare input for Gephi:

Gephi (Java 1.8 or higher) is a nice visualization tool for graphical data.
We’ll output our data into a format recognizable by Gephi.

id_to_named_entity = {named_entity_id: named_entity
                      for named_entity, named_entity_id in tokenizer.items()}

with open('clusters.gdf', 'w') as f:
    f.write('nodedef>name VARCHAR,cluster_id VARCHAR,label VARCHAR\n')
    for index, row in clusters_df.iterrows():
        f.write('{},{},{}\n'.format(row['named_entity'], row['cluster'], id_to_named_entity[row['named_entity']]))
    f.write('edgedef>node1 VARCHAR,node2 VARCHAR, weight DOUBLE\n')
    for index, row in edges_df.iterrows(): 
        f.write('{},{},{}\n'.format(row['named_entity_1'], row['named_entity_2'], row['weight']))

Finally, we can open clusters.gdf using Gephi in order to inspect the clusters.

附录

参考文献

Wang, Minjie, Quan Gan, Jake Zhao, and Zheng Zhang. 2019. “DGL at a Glance.” DGL. 2019. https://docs.dgl.ai/tutorials/basics/1_first.html#sphx-glr-tutorials-basics-1-first-py.

苘郁蓁. 2019. 机器学习算法与自然语言处理. 2019. https://mp.weixin.qq.com/s/DWfgOW7whkImNLSCLhQL7A.