决策树、随机森林学习笔记
2020-02-23
- 使用 RMarkdown 的
child参数,进行文档拼接。 - 这样拼接以后的笔记方便复习。
- 相关问题提交到 GitHub
Hartshorn (2016) 是博客的串联,并且只有60多页,但是 用图解释决策树、随机森林还是不错的。
1 决策树的训练过程
假设四种水果, 苹果、橙子、香蕉、柚子。 数量和对应的颜色分别是,
| 品种 | 样本数量 | 颜色 |
|---|---|---|
| 苹果 | 24 | 红、绿、黄 |
| 橙子 | 24 | 橙 |
| 香蕉 | 19 | 黄、绿 |
| 柚子 | 21 | 橙、黄 |
这里的特征变量颜色暂时没有使用到,我们只用它们的长宽来进行分类。看图。
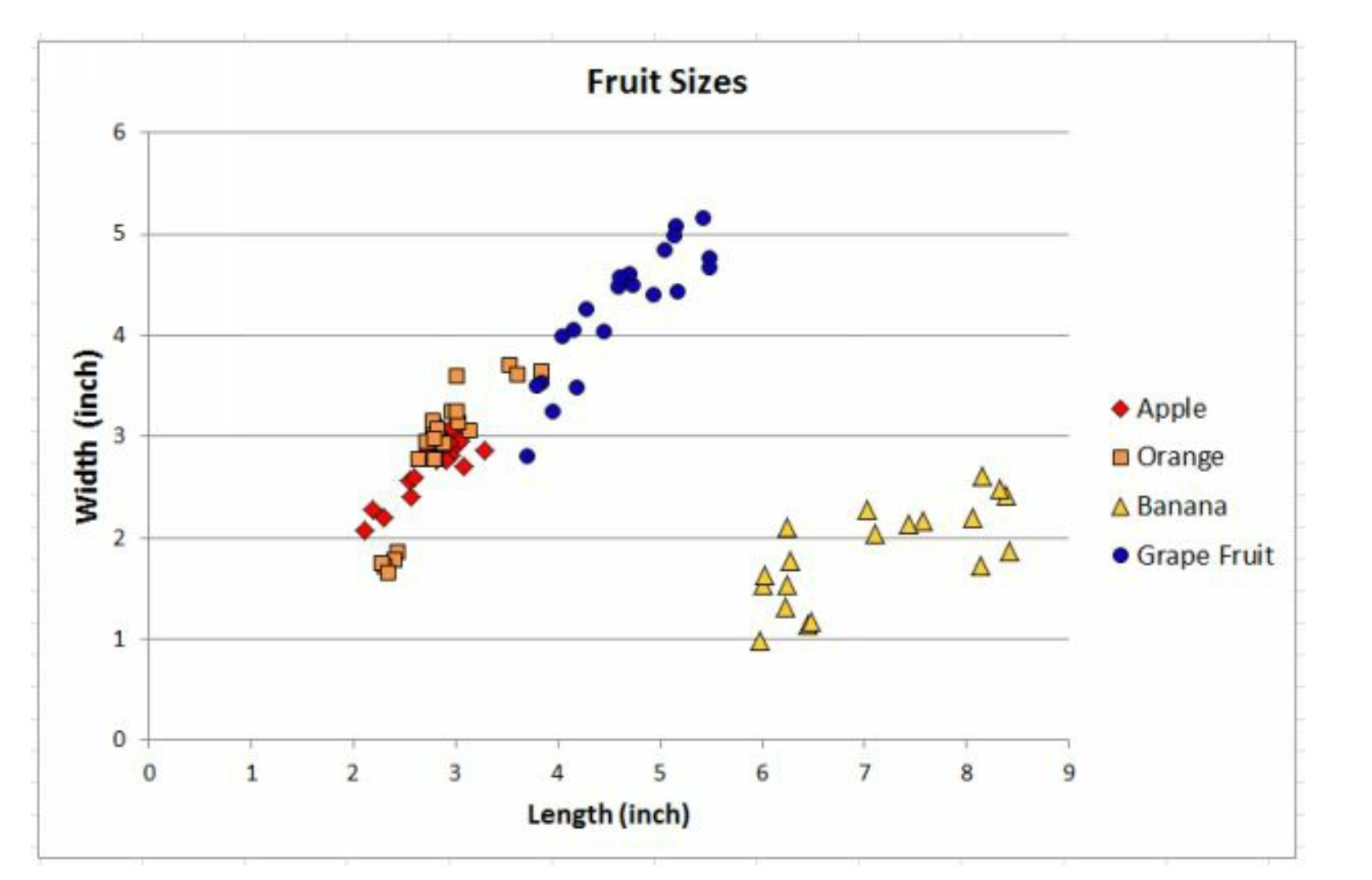
这里Grape Fruit是柚子。
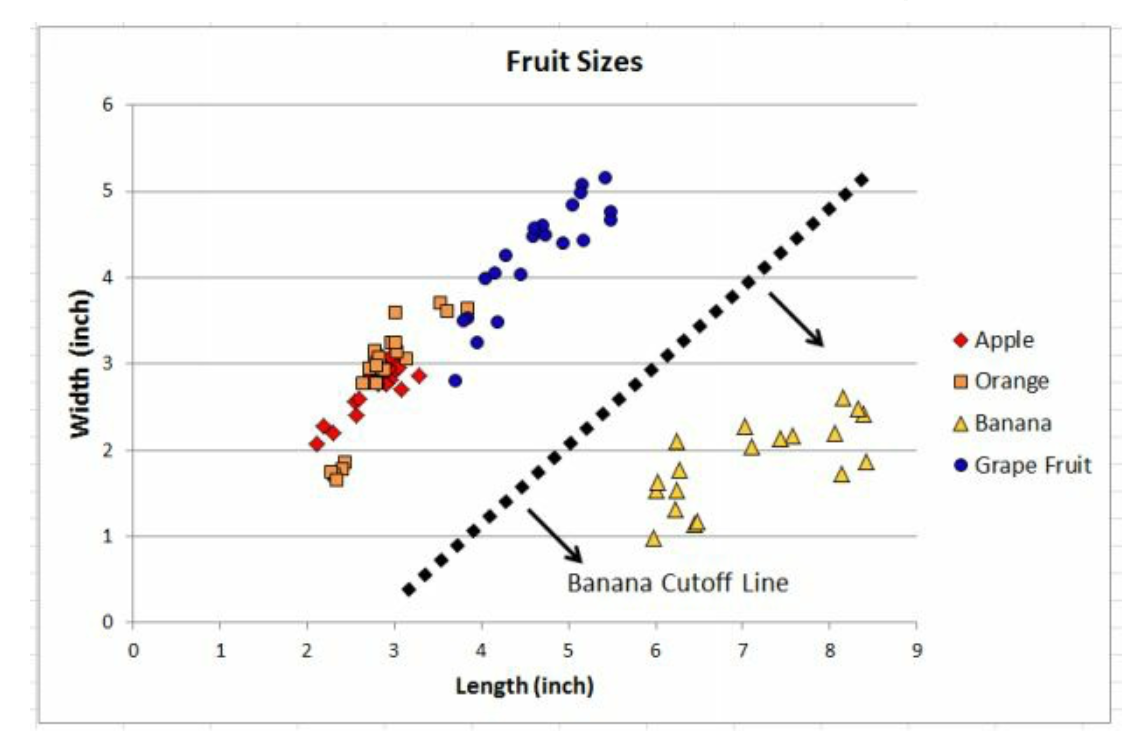
显然我们可以一刀把香蕉分出来。1
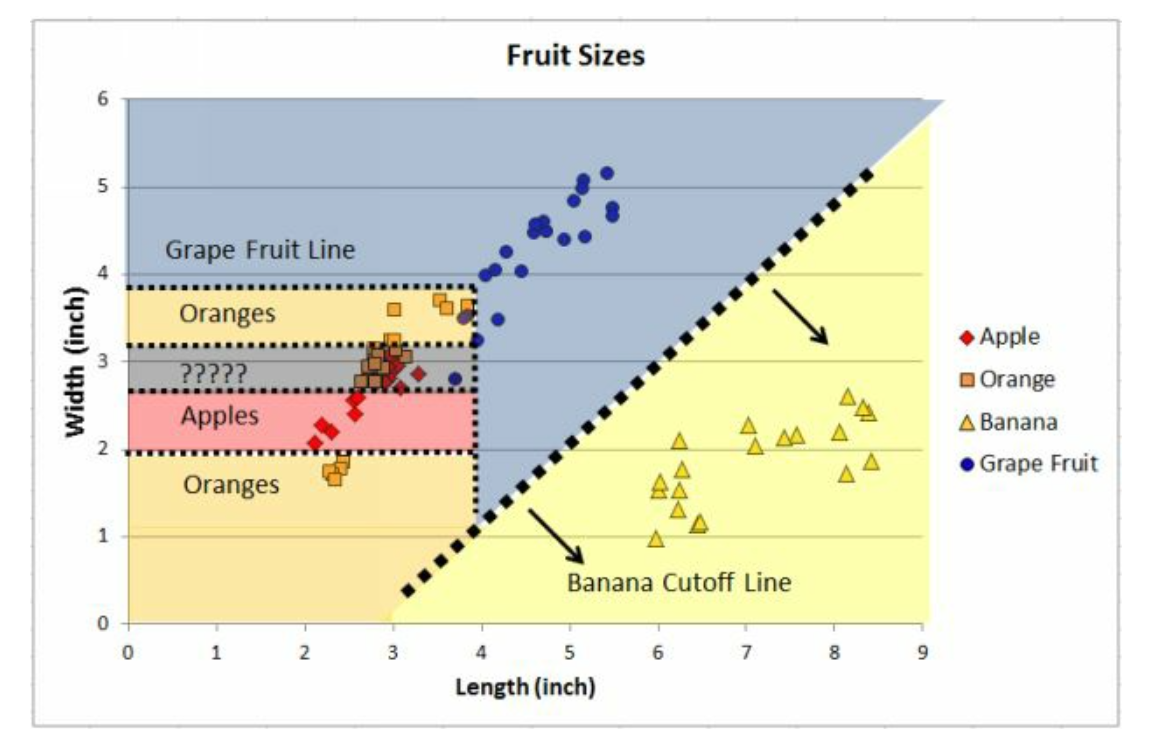
重复操作。我们几刀下来如上图。
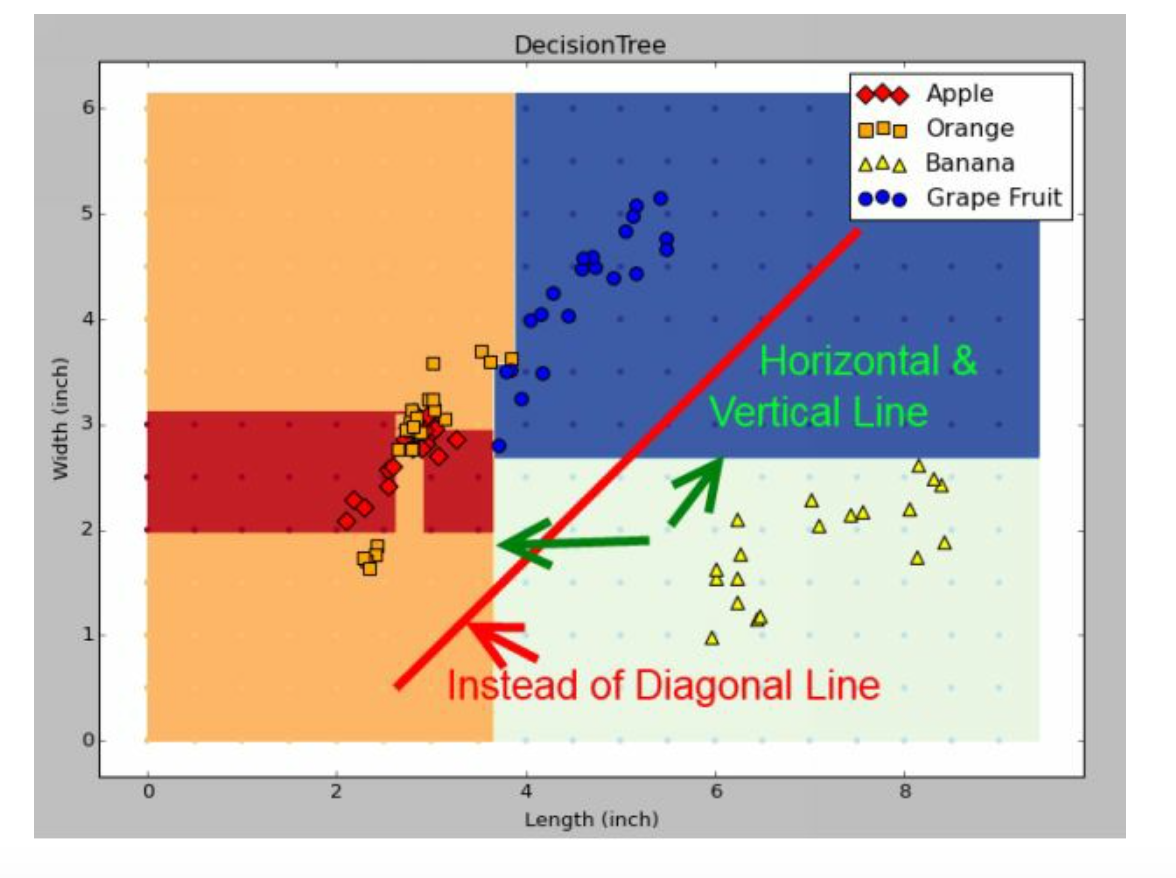
但是实际上决策树不能够斜着切,因为每一刀都是选择一个变量进行切 split,因此实际上我们只能横纵切,可以理解为棋盘。
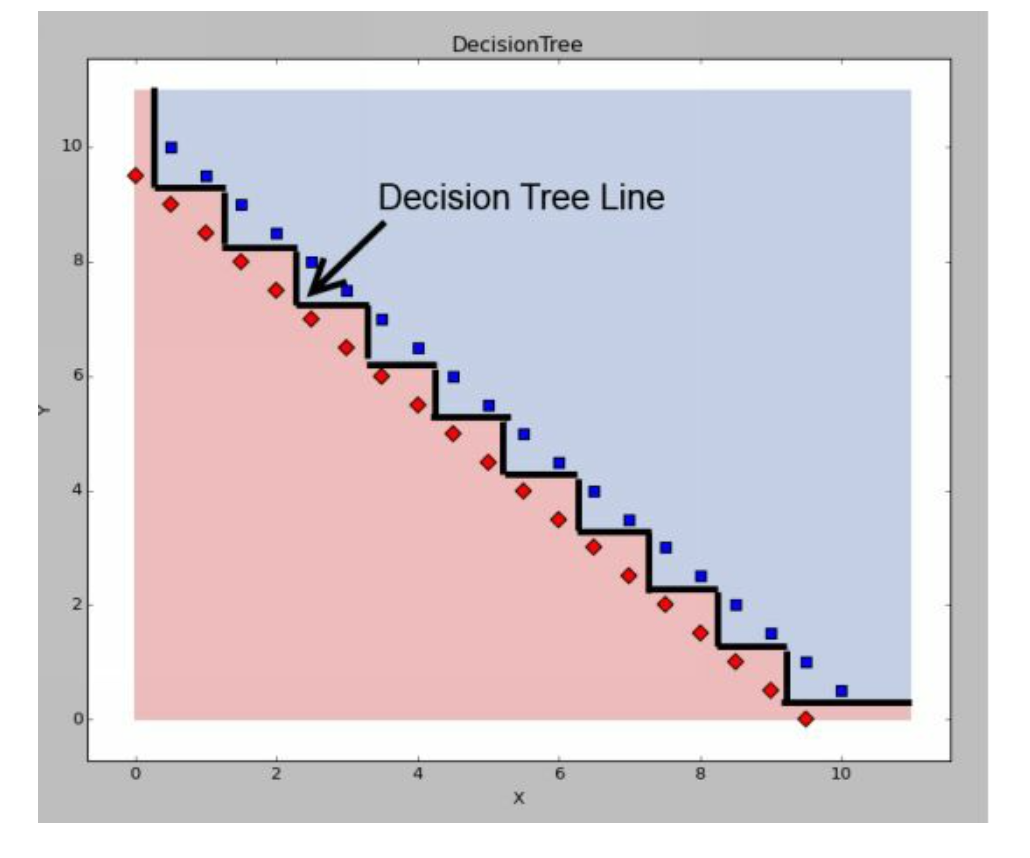
实际上的斜线是锯齿状的,和经济学里面需求供给曲线类似。
2 过拟合的直观理解
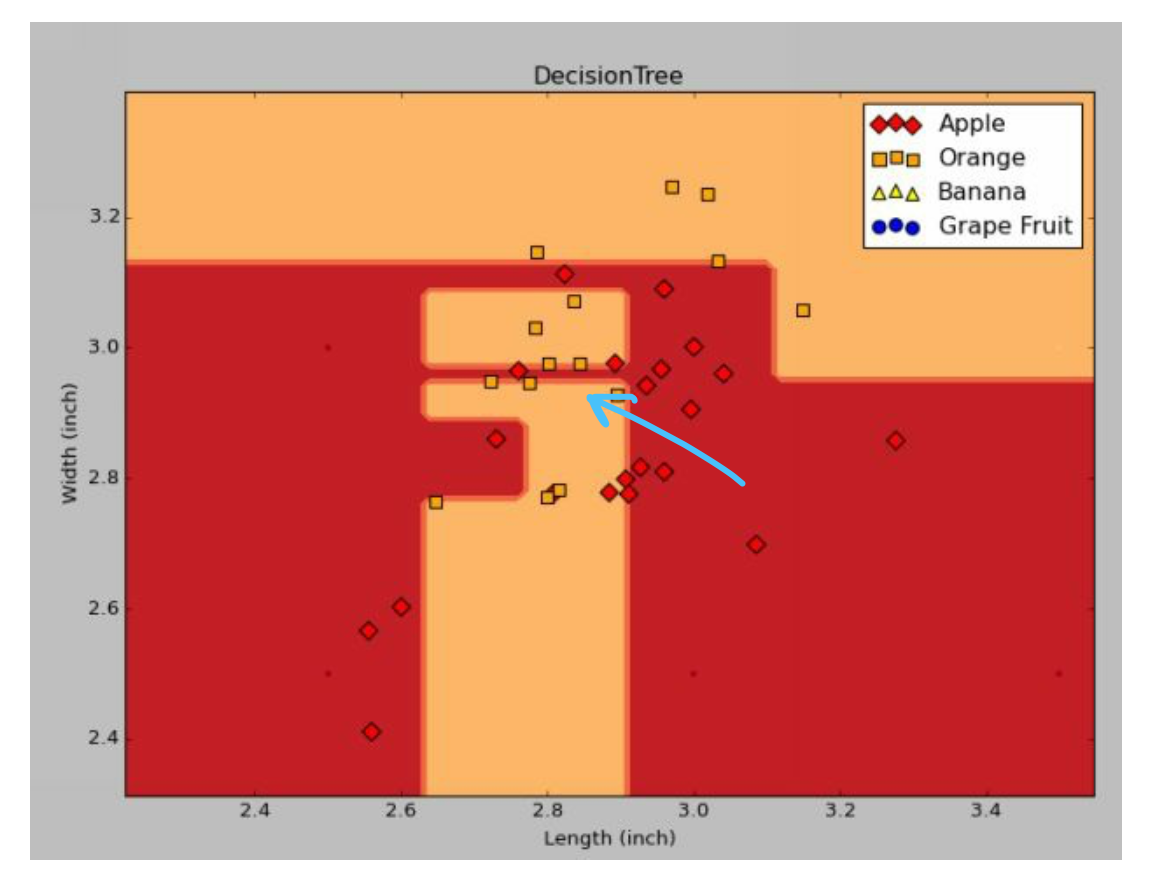
我们把分不清楚那部分拿出来看, 要是非要100%切好,那么100%正确率了。 但是泛化能力就低了。也就是说给一个随机水果过来, 根据长宽来判断,那么误差一点点,可能就分错了, 因此需要其他稀疏一点的变量来区分,即使误差一点点,但是也不会分错。 举个例子,注意蓝色那条线,实际上,苹果在这是2.87 inchs, 但是只要random过来的苹果是2.86 和 2.88 inchs,就会划分到橙子那里去了。 因此过拟合很严重。
3 Bagging 图像理解
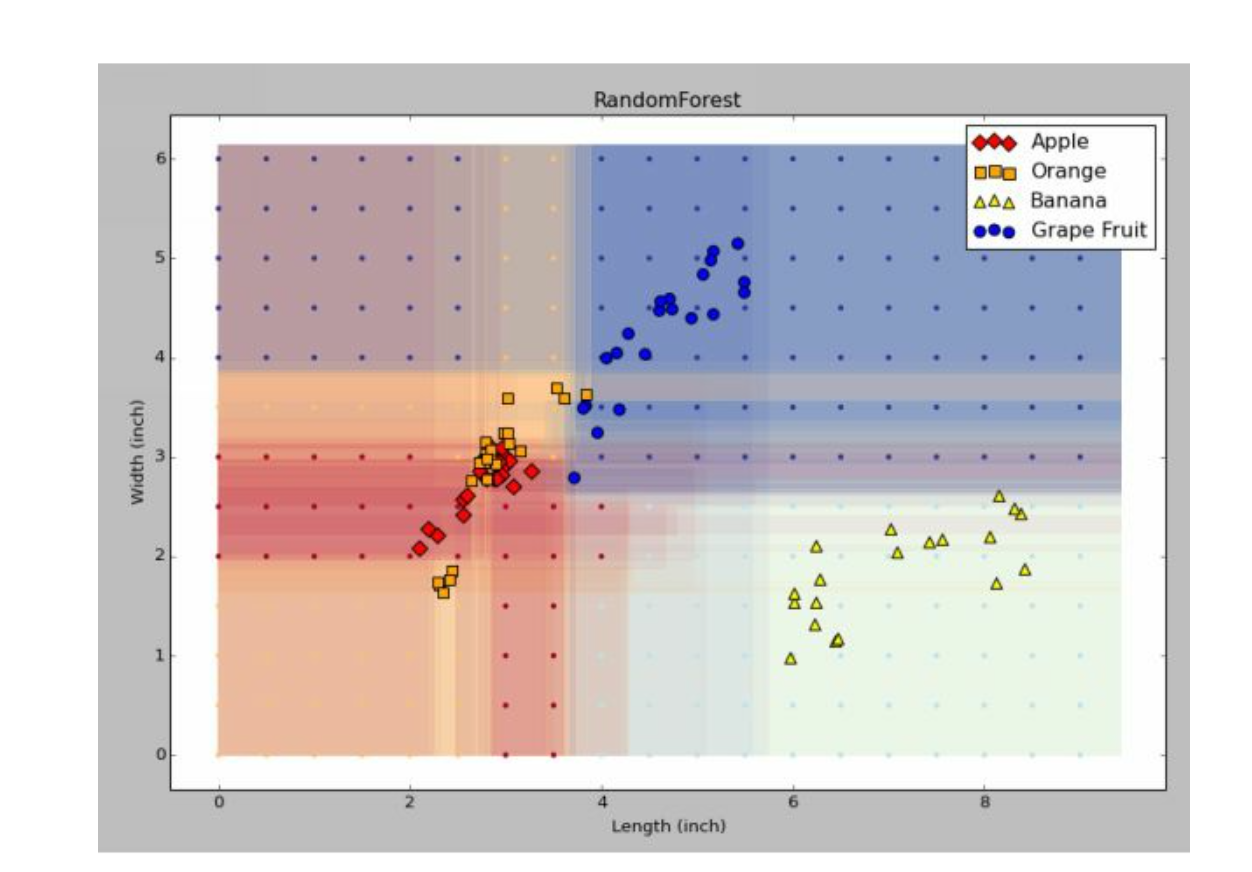
我们对样本进行了0.8倍的bagging,产生了17个决策树,将图像叠层后出现这样的。 显然颜色清晰的就是100%确定的,模糊的,就需要估计一个各个类别的概率了。
接下来主要讲
- 为什么随机森林对异常值处理效果好,
- 为什么importances受到变量相关性影响很大,
- 两种信息计算方式
- 随机森林处理线性问题的bug
3.1 为什么随机森林对异常值处理效果好
随机森林是bagging的加强版,加入了变量的随机抽样。 我们知道,bagging就是要对样本重复抽样,那么理论上异常值是少数的,那么被随机选到概率极低,因此bagging使得异常值对模型的影响几乎很小。
3.2 为什么随机森林让好的变量脱颖而出
随机森林在 bagging 基础上加入了变量的随机抽样, 那么好的变量是总是能够从不同的树中脱颖而出,因为机会更多了嘛,而不是决策树只有一次机会。 所以比较好的情况是,从100个树逐渐增加树,当然这可能让一些指标变差,因为 异常 的好情况可能会被smoothing掉,但是结果的泛化能力也会更好。
4 什么是 out of bag error
当重复抽样时,例如,从原来样本选择60%的样本作为的一个bag1,那么剩下的40%就可以作为out of bag,来作为这个bag的测试组。
\[\begin{matrix} original \to & 60\%&bag_{1} & 60\%&bag_{2} & \cdots \\ & 40\%&O.O.B_{1} & 40\%&O.O.B_{2} & \cdots \\ \end{matrix}\]
5 如何确定每一刀怎么切
5.1 基尼系数
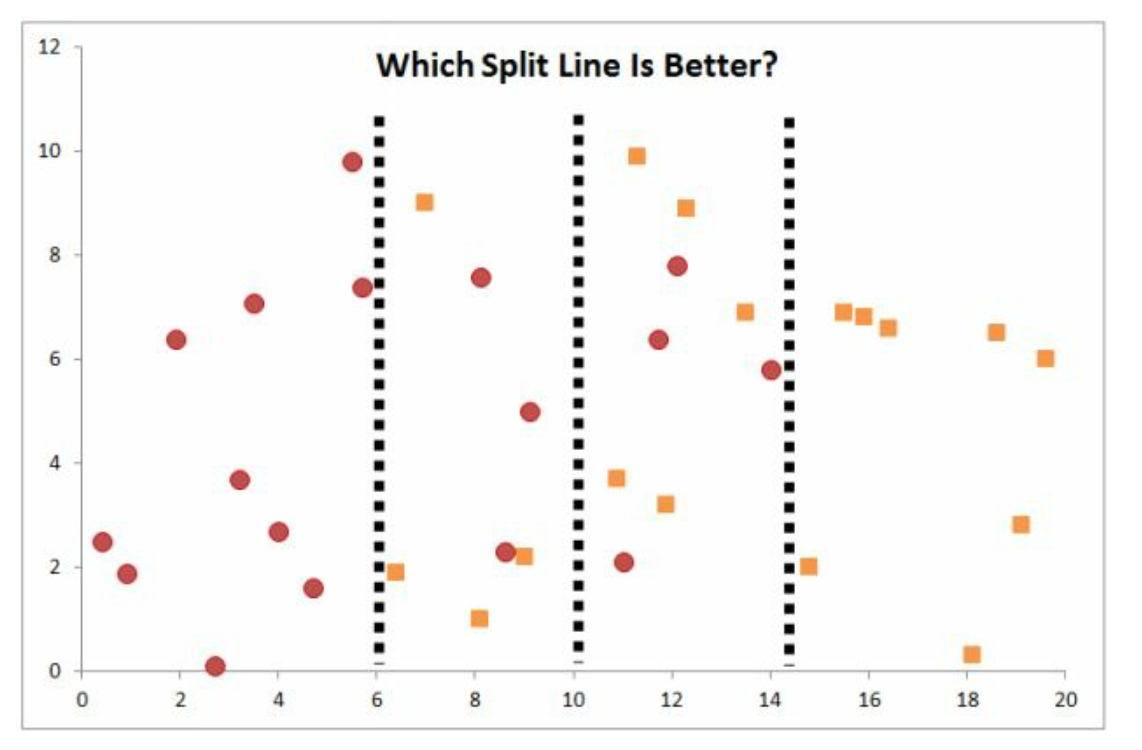
如图这第一刀到底切哪呢?
我们定义基尼系数,来作为选拔标准。
\[Gini = 1- \sum{j=1}p_j^2\]
Gini衡量了此时此刻,这个节点的样本的异质性。 如果样本越纯粹,那么Gini越小,越好。 这里的\(j\)表示这个节点,样本的\(y\)类别。 比如我们的训练样本里面\(y = A,B,C,D\)。在这个节点\(y\)有三种, \(B,C,D\),那么这里的\(j=1,2,3\),其中\(p_j\)代表各类别(class)在节点样本中的比例。
我们可以举一个例子。
假设在这个节点有如下样本
- 苹果10个
- 香蕉6个
- 椰子4个
因此在节点他们的比例为
- 苹果0.5
- 香蕉0.3
- 椰子0.2
因此基尼系数(Gini Impurity),
\[Gini = 1 - (0.5^2 + 0.3^2 + 0.2^2) = 0.62\]
显然够杂乱的,如果是\(0\)是最好了,说明样本中100%是同一类,那么\(Gini = 1 - (1^2 + 0^2 + 0^2) = 0\)。因此样本在类别间越平均,Gini越高。 \(Gini \n [0,1]\)。
然后,假设我们某刀这么切,
注意这里只切了一刀。
那么我们开始计算切以后的Gini系数了。
左边
\[Gini_1 = 1 - ((\frac{2}{3})^2 + (\frac{1}{3})^2 + 0^2) = 0.444\]
右边
\[Gini_1 = 1 - {0 + (\frac{1}{5})^2 + (\frac{4}{5})^2} = 0.32\]
所以加权后是
\[W.A.Gini = \frac{0.444\times 15 + 0.32 \times 5}{15+5} = 0.413\]
因此Gini在切以后,从0.62变到了0.413,因此是有效的。
这里的信息增益 Info.Gain = 0.62 - 0.413 = 0.207。
那这说明什么呢?
如果某一刀能够使得切以后的Gini系数更小,也就是说同质性更高,那么这一刀就更好,相应的获得的info.gain越高。 在最后评importance打榜的时候,越有用。
总结,对于每个节点,都对应一个Gini系数。 Gini系数越高,反映样本在不同类别之间分布均匀,这个节点的样本分的不好。 Gini系数越低,反映样本在不同类别之间分布集中于某个类别,这个节点的样本不需要再切。 对于某刀能够让Gini系数下降最快,也就是说让切了以后的节点都达到比较高的同质性,那么这刀效果就好。
5.2 Entropy信息熵的方法
这里就定义了
\[Entropy = \sum_{j=1}-p_i\log_2{(p_j)}\]
\(Entropy \in [0,1]\)也是越小越好,说明同质性越高。
6 Importances 计算逻辑
Importances的好处是,让我们在有限的时间内集中于关注哪些变量。 但是因为最后的计算要标准化,因此如果变量之间有很强的相关性,那么最后importance会被平分,导致一个很重要的变量,被两三个相关性很强的瓜分了,结果排名很靠后,这个地方看不懂后面具体介绍。
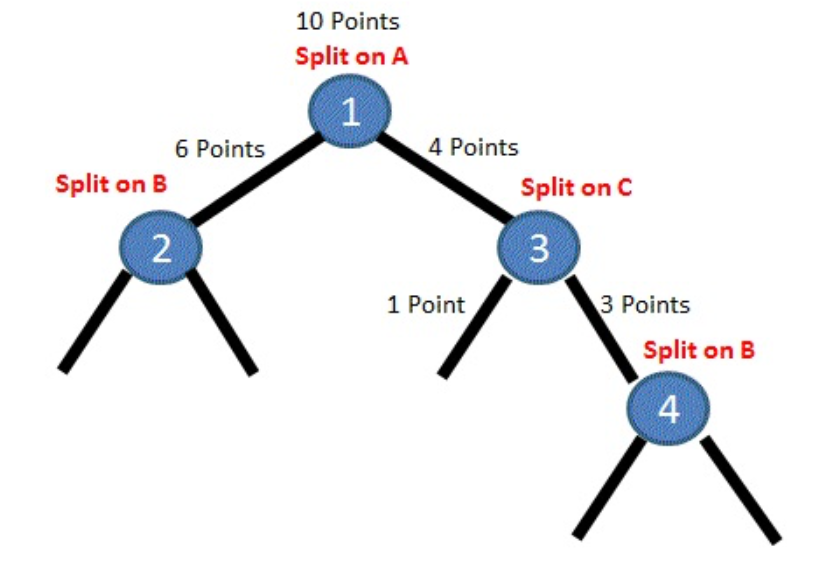
如图,有四刀产生,其中第一刀,把10个样本分成了6个一类和4个一类。 每一刀代表一个变量,那么我们一共去计算这些变量产生的信息增益。
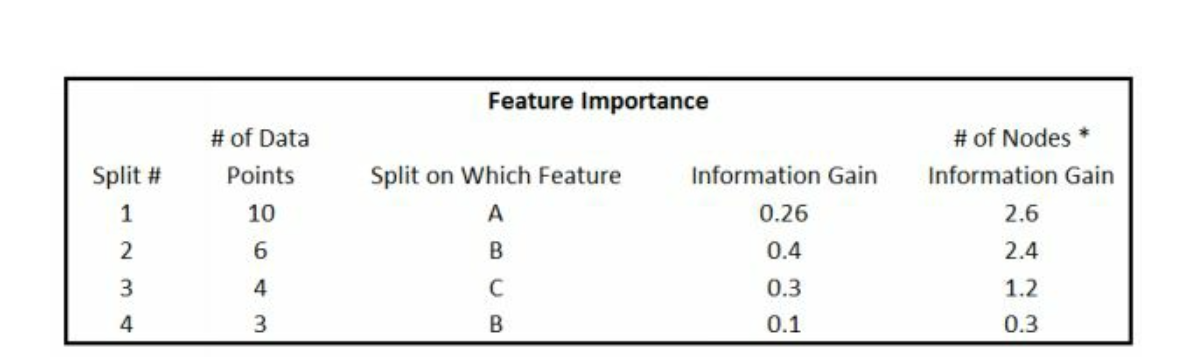
例如,假设第一刀是通过变量A实现的,产生了0.26的信息增益,因为我们知道信息增益\(Info.Gain \in [0,1]\),反映的是平均状态,因此需要乘上样本数,变成2.6。 同理每刀都计算信息增益和样本数。
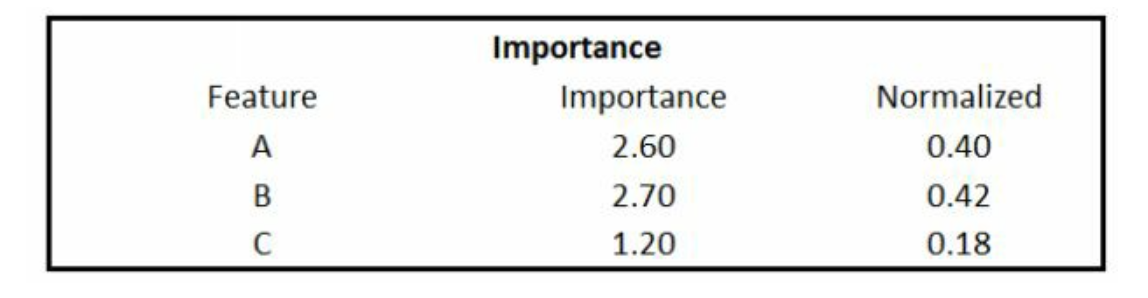
最后我们按照变量进行汇总,然后标准化,如图。 我们认为B因为标准化后最高,因此最重要,这就是importances。
最后我们知道随机森林,会产生若干的bag,然后每个bag会随机抽样不同的变量, 那么这里每个树,都可以做以上的计算,那么之后每个变量,可以求平均的importances。 由于在每个树里面importances是标准化后的,因此均值也是\(\in [0,1]\)。 由于变量在随机抽样的是,概率相等,因此这里很公平。
但是这里存在一个bug。 如果我们的变量里面有两个变量相关性是1,那么它们被随机抽中的概率相等,在随机森林中发挥这相同的功效,在每个树里面,它们会经过标准化,那么importances就会降一半。
例如,
| 变量 | Imortances | 标准化后 |
|---|---|---|
| A | 2.7 | 0.40 |
| B | 0.5 | 0.07 |
| C | 0.8 | 0.12 |
| A1 | 2.7 | 0.40 |
但是实际上
| 变量 | Imortances | 标准化后 |
|---|---|---|
| A | 5.4 | 0.81 |
| B | 0.5 | 0.07 |
| C | 0.8 | 0.12 |
因此A因为A1缩小了一般的重要性,因此在重要性排名的时候,就会非常落后。
因此或许相关性很高的变量似乎不会影响模型,因为用A和用A1都可以的。
不影响预测能力,但是会对我们选择最好的变量产生很大的影响,
也许有个变量很好,但是被替身抢了一般的功劳。
再举个例子,比如,以前就是LH很红,那么他可能排在前三,自从有了GXT,那么它们相关性很高,因此重要性分了一半,那么LH的重要性降低一半。
因此当样本中高相关性的特征向量时,这种共线性问题不影响模型的性能 (DMLC 2016)。
7 随机森林只能预测训练集有的值
随机森林直接接受连续变量,因此我们需要讲分类变量连续化,as.integer。
或者我们觉得连续变量不单调稳定,也是先切bin,变成分类变量再变成连续变量,这里就产生了bug。
例如我们有数据 工作一小时10美元,以下这样表示,
- $10 1hr
- $20 2hr
- $30 3hr
线性回归是10hr \(\to\) $100。 但是这里只会反馈$30。 因此随机森林处理线性问题有时候近乎智障。
参考 cran

image
如图 xgb 和 rf 就不会去预测太高的值。
8 调整参数
considering around 300 trees and min samples leaf equal to 1 Rule of thumb: The more estimators, the better, up to a certain plateau, after which 2000 or 10000 estimators do not make a difference, and the score could even show a dip. https://www.kaggle.com/general/4092
? 查询参数意思。基本上 300 差不多,1000+ 以后的意义不大。
随机森林太容易过拟合了,超参数太重要了,sklearn 给的默认太差了,一定要自定义好过拟合参数。
DMLC. 2016. “Understand Your Dataset with Xgboost.” 2016. http://xgboost.readthedocs.io/en/latest/R-package/discoverYourData.html.
Hartshorn, Scott. 2016. Machine Learning with Random Forests and Decision Trees: A Visual Guide for Beginners. Amazon Digital Services LLC.
注意这种斜着切的,实际上需要迭代,在随机森林里面实现。决策树只能横着和竖着切。↩