辛普森悖论 学习笔记

李家翔

2019-12-02

1. 使用 RMarkdown 的 child 参数，进行文档拼接。
2. 这样拼接以后的笔记方便复习。
3. 相关问题提交到 Issue

辛普森悖论主要两个体现：权重扭曲和遗漏变量。

1 权重扭曲

辛普森悖论跟条件期望和无条件期望。

无条件期望由条件期望所决定，但别忘了 “权重”依然起着重要的作用。 (陈强 2019)

考虑一个例子，

全班平均成绩=男生平均成绩和女生平均成绩的加权平均

进一步，假设 A 班的男生平均成绩高于 B 班的男生平均成绩；而 A 班的女生平均成绩也高于 B 班的女生平均成绩。因此，从条件期望的角度，A 班完胜 B班。 (陈强 2019)

但是权重的不同，可能逆转无条件期望的结果。

那么，从无条件期望的角度，B 班是否有可能超过 A 班呢？换言之，B 班的全班（含男女生）平均成绩是否依然可能高于 A 班的全班平均成绩呢？依然有可能！只要 B 班的高分女生所占比重足够大，而 A 班的高分女生所占比重足够小。 (陈强 2019) 这种可能性的存在意味着，即使总体 A 的条件期望总是大于总体 B 的条件期望，而由于总体每种 “条件” 的发生概率（比重）不同，使得在将 “部分” 加总之后，所得的 “整体” 结果可能逆转。 (陈强 2019)

这就是“辛普森悖论”（Simpson’s Paradox）的一种情况。

这种从部分到整体所可能发生的 “逆转” (陈强 2019)

权重的扭曲。 因此很多常识上是错误判断，如部分和整体的不一致，辛普森悖论就是一种情况。

1.1 应用一

辛普森悖论的一个著名案例涉及 1973 > 年加州大学伯克利分校的研究生入学是否存在性别歧视。该年的研究生录取记录显示，男生的录取率为 44%（共8442 名男生申请），而女生的录取率仅为 35%（共 4321 名女生申请），不同性别的录取率显然存在显著差异。 (陈强 2019)

论点是性别歧视。 但是男女录取率的差异是否就是歧视呢? 男女这个 total set，对呢?还是需要subset 一下? subset 的结论是否还一致? 不一致就是权重差异，就是整体和部分不一致的一种情况。

然而，进一步考察发现，在伯克利大学的 85 个系中，有 6 个系的女生录取率显著高于男生，而只有 4 个系的男生录取率显著高于女生；而在其他系中，男女生的录取率并无显著差别。 (陈强 2019) 事实上，之所以女生的整体录取率明显低于男生，主要是因为女生倾向于申请竞争激烈而录取率低的专业（比如英文），而男生则倾向于申请竞争较少而录取率高的专业（比如工程与化学）。如此看来，伯克利大学的所谓 “性别歧视” 正是辛普森悖论所导致的乌龙。 (陈强 2019)

我觉得是这四个系招人很多，扭曲了权重。

另外申请难度不一致，不公平吧，应该 partial 掉申请难度，遗留变量是辛普森悖论的另外一种体现，这个后面再讲。

1.2 应用二

个人在做决策时，也可能受到辛普森悖论的影响。假设你有一位朋友生病，需要在 A 医院与 B 医院中选择一家。此时，你知道 A 医院的死亡率高于 B 医院，是否你一定会向朋友推荐 B医院？ (陈强 2019)

不，朋友是一个subset的范畴，整体和部分可以不一致。

不妨假设病人可分为两类，即 “重病号” 与 “轻病号”。事实上，可能存在这样一种可能性，不仅 A 医院的重病号死亡率低于 B 医院，而且 A医院的轻病号死亡率也低于 B 医院。只是由于很多死亡率高的重病号选择去 A 医院，才导致 A 医院的整体死亡率较高。 (陈强 2019) 如此看来，你在向朋友推荐医院时，确实需要小心。此例也告诉我们，在做决策时，一般来说 “条件期望” 比 “无条件期望” 包含更多信息，你需要根据自己的 “条件” 使用条件期望来做出最优决策。在此例中，无论你的朋友是重病号，还是轻病号，都应该去 A 医院（假设 A 医院的重病号与轻病号死亡率都更低）。 (陈强 2019)

这是一种思路，在产品上落地时，要考虑权重扭曲的情况，整体和部分不一定结论一致。

在现实中，也有可能出现这样一种情况，即 A医院的重病号死亡率更低，而 B 医院的轻病号死亡率更低；那么你在做决策时，就应该根据自己的情况（究竟是重病号还是轻病号），对号入座。当然，如果你缺乏条件期望的信息，那么就只能根据无条件期望做大致的判断，因为在大多数情况下，二者还是一致的（如果权重的分布不过于扭曲）。 (陈强 2019)

所以辛普森悖论的一种情况是权重分布扭曲导致的。

2 遗漏变量

参考 Holtz and Healy (2019)

library(tidyverse)
library(hrbrthemes)
library(babynames)
library(viridis)
library(tidyverse)

a <-
    data.frame(x = rnorm(100), y = rnorm(100)) %>% mutate(y = y - x / 2) %>% mutate(group = 'A')
b <-
    a %>% mutate(x = x + 2) %>% mutate(y = y + 2) %>%  mutate(group = 'B')
c <-
    a %>% mutate(x = x + 4) %>% mutate(y = y + 4) %>%  mutate(group = 'C')
data <- bind_rows(a, b, c)

p1 <- ggplot(data, aes(x = x, y = y)) +
    geom_point(size = 2) +
    theme_ipsum() +
    geom_smooth(method = "lm")

p2 <- ggplot(data, aes(x = x, y = y, color = group)) +
    geom_point(size = 3) +
    scale_color_viridis(discrete = TRUE) +
    geom_smooth(method = "lm") +
    geom_smooth(aes(x =x ,y=y), data, method = "lm") +
    theme_ipsum()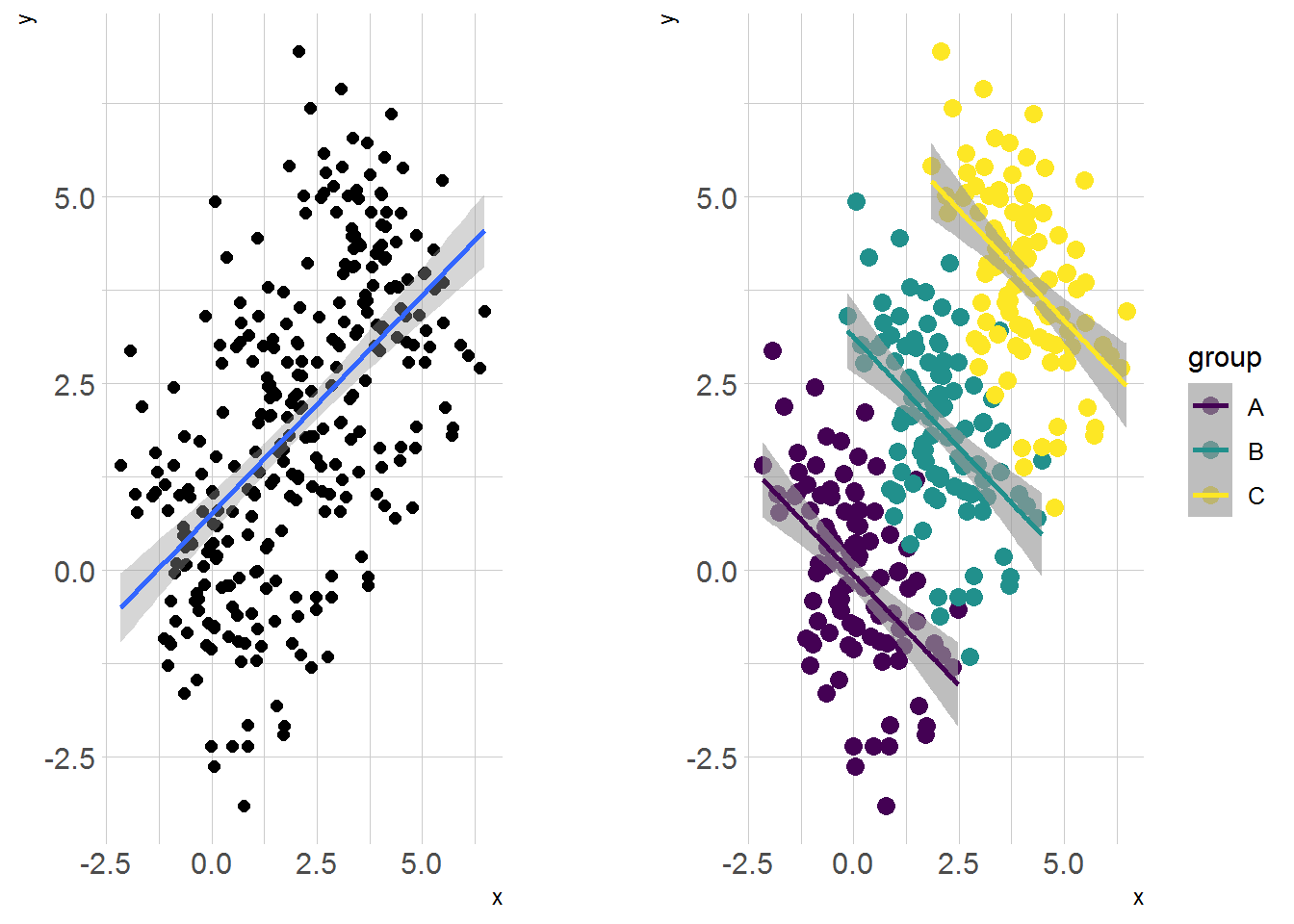

library(patchwork)
p1 + p2

这个图整体和部分的不一致，不算是权重扭曲了，但是也是辛普森悖论的另外一种体现。 每个局部完全和整体不一致。

此时，混合回归相当于 “无条件期望”，因为没有控制企业的个体固定效应（individual fixed effects），故无法反映变量 x 对于变量 y 的真实作用（混合回归一般不一致）。而个体固定效应模型则相当于 “条件期望”，因为控制了企业的个体固定效应，故可以得到一致估计。 (陈强 2019)

因此 between 的固定效应模型处理后，就可以算出正的斜率了，因为都减去了各自的均值。

df2 <-
    data %>%
    group_by(group) %>%
    mutate(x = x - mean(x),
           y = y - mean(y))

p1 <- ggplot(df2, aes(x = x, y = y)) +
    geom_point(size = 2) +
    theme_ipsum() +
    geom_smooth(method = "lm")

p2 <- ggplot(df2, aes(x = x, y = y, color = group)) +
    geom_point(size = 3) +
    scale_color_viridis(discrete = TRUE) +
    geom_smooth(method = "lm") +
    geom_smooth(aes(x =x ,y=y), df2, method = "lm") +
    theme_ipsum()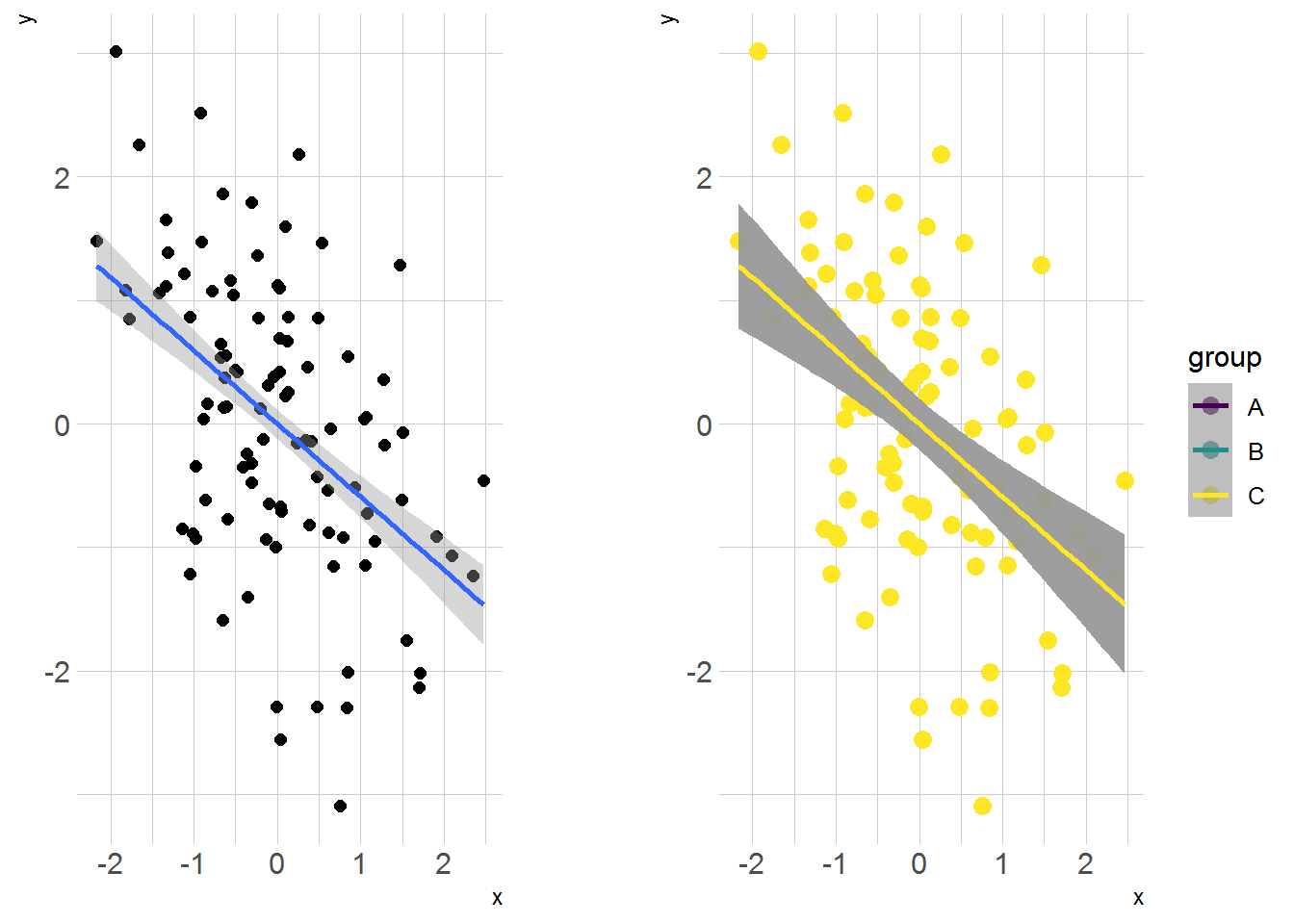

library(patchwork)
p1 + p2

由此可知，辛普森悖论的另一解释角度为 “遗漏变量偏差”（omitted variable bias）；在理论上，如果能控制足够多的条件，则可以避免。 (陈强 2019)

因此单纯的看整体，不做回归，是看不到局部影响的。 这也是 pooled regression 和 between 的差异。

between 处理后，回归的斜率就是体现个体效应的了。

2.1 EDA的启示

总结来看，这种看散点图做变量的方法有弊端 一般都会产生辛普森悖论。

这里会把相关性判断反，因此需要剔除固定效应模型，但是一般散点图不会告诉使用者是否需要做固定效应模型，这都是需要对应的检验发现的。 这也是 Thomas Loeber 大体说下来的内容。

Likewise, I would use a more formal procedure for feature selection and be very hesitant to throw away any data. Even if multiple predictors are strongly correlated, it is hard to say intuitively what threshold to use. So I would include them all, and if the regression coefficients of the respective variables are unstable, I would see how much worse the model performs (again using withheld data) if I just use one. An even better solution would be to extract the principal components and use those as predictors instead. (Thomas Loeber)

这里强调需要一个统一的框架进行特征筛选，而不是这种一个个 y ~ x 去隔离的进行。

附录

参考文献

Holtz, Yan, and Conor Healy. 2019. “THE Simpson’S Paradox.” From Data to Viz. 2019. https://www.data-to-viz.com/caveat/simpson.html.

陈强. 2019. “一石二鸟：从迭代期望定律透视辛普森悖论.” 计量经济学及Stata应用. 2019. https://mp.weixin.qq.com/s/_VIROvJmBkvWpi6DExFOWA.